AI 從頭學(2020 年版)
2019/08/14
-----
-----
一、精華篇
(一)AI 三部曲(深度學習:從 CV 到 NLP)
https://hemingwang.blogspot.com/2019/05/trilogy.html
(二):BERT Overview
https://hemingwang.blogspot.com/2019/01/bert-overview.html
(三):History of Natural Language Processing
https://hemingwang.blogspot.com/2019/01/history-of-natural-language-processing.html
(四)深度學習論文下載
http://hemingwang.blogspot.com/2019/02/deep-learning-highlight.html
-----
二、基礎篇
(一):文獻回顧
http://hemingwang.blogspot.com/2016/12/ai.html
(二):Popular Deep Learning Software Tools
http://hemingwang.blogspot.com/2016/12/aipopular-deep-learning-software-tools.html
(三):Popular Deep Learning Hardware Tools
http://hemingwang.blogspot.com/2016/12/aipopular-deep-learning-hardware-tools.html
(四):AD and LeNet
http://hemingwang.blogspot.com/2016/12/aiad-and-lenet.html
(五):AD and Python
http://hemingwang.blogspot.com/2016/12/aiad-and-python.html
(六):The Net
http://hemingwang.blogspot.com/2016/12/aithe-net.html
(七):AD and Python from Jason
http://hemingwang.blogspot.com/2016/12/aiad-and-python-from-jason.html
(八):The Net from Mark
http://hemingwang.blogspot.com/2016/12/aithe-net-from-mark.html
(九):Back Propagation
http://hemingwang.blogspot.com/2017/02/aiback-propagation.html
(一0):Automatic Differentiation
http://hemingwang.blogspot.com/2017/02/aiautomatic-differentiation.html
(一一):A Glance at Deep Learning
http://hemingwang.blogspot.com/2017/02/aia-glance-at-deep-learning.html
(一二):LeNet
http://hemingwang.blogspot.com/2017/03/ailenet.html
(一三):LeNet - F6
http://hemingwang.blogspot.com/2017/03/ailenet-f6.html
◎ LeNet 的補充
http://hemingwang.blogspot.com/2018/02/deep-learninglenet-bp.html
(一四):Recommender
http://hemingwang.blogspot.com/2017/03/ai.html
(一五):Deep Learning,How?
http://hemingwang.blogspot.com/2017/03/aideep-learninghow.html
(一六):Deep Learning,What?
http://hemingwang.blogspot.com/2017/03/aideep-learningwhat.html
(一七):Shallow Learning
https://hemingwang.blogspot.com/2017/03/aishallow-learning.html
(一八):Convolutional Neural Network
http://hemingwang.blogspot.com/2017/03/aiconvolutional-neural-network_23.html
(一九):Recurrent Neural Network
http://hemingwang.blogspot.com/2017/03/airecurrent-neural-network.html
◎ RNN 的補充
http://hemingwang.blogspot.com/2018/02/airnnlstmin-120-mins.html
(二0):Deep Learning,Hot
http://hemingwang.blogspot.com/2017/03/aideep-learninghot.html
(二一):A Glance at Deep Reinforcement Learning
http://hemingwang.blogspot.com/2017/04/aia-glance-at-deep-reinforcement.html
(二三):CNN - Kernel Training
http://hemingwang.blogspot.com/2017/05/aicnn-filter-kernel-training.html
(二四):CNN - Kernel Visualizing
http://hemingwang.blogspot.com/2017/05/aicnn-filter-kernel-visualizing.html
◎ CNN 的補充
http://hemingwang.blogspot.com/2018/02/deep-learningcnn.html
(二五):AlphaGo
http://hemingwang.blogspot.com/2017/05/aiaja-huang.html
(二六):AlexNet
http://hemingwang.blogspot.com/2017/05/aialexnet.html
(二七):ZFNet
http://hemingwang.blogspot.com/2017/05/aikernel-visualizing.html
(二八):Network in Network
http://hemingwang.blogspot.com/2017/06/ainetwork-in-network.html
(二九):GoogLeNet
http://hemingwang.blogspot.com/2017/06/aigooglenet.html
(三0):Conv1
http://hemingwang.blogspot.com/2017/06/aiconv1.html
(三一):Inception
http://hemingwang.blogspot.com/2017/08/aiinception.html
(三二):VGGNet
http://hemingwang.blogspot.com/2018/09/aivggnet.html
(三三):ResNet
http://hemingwang.blogspot.com/2018/09/airesnet.html
(三四):FCN
http://hemingwang.blogspot.com/2018/02/deep-learningfcn.html
(三五):DPM
http://hemingwang.blogspot.com/2017/07/aiobject-detection-with.html
(三六):YOLO v1
http://hemingwang.blogspot.com/2018/04/deep-learningyolo-v1.html
◎ YOLOv1 的補充:mAP
http://hemingwang.blogspot.com/2018/04/machine-learning-conceptmean-average.html
◎ YOLOv1 的補充:NMS
http://hemingwang.blogspot.com/2018/04/machine-learning-conceptnon-maximum.html
(三七):Weight Decay
https://hemingwang.blogspot.com/2017/06/aiweight-decay.html
(三八):Highlight
http://hemingwang.blogspot.com/2017/11/aihighlight.html
(三九):Complete Works
http://hemingwang.blogspot.com/2017/08/aicomplete-works.html
-----
三、進階篇
NLP(一):LSTM
https://hemingwang.blogspot.com/2019/09/lstm.html
NLP(二):Seq2seq
https://hemingwang.blogspot.com/2019/09/seq2seq.html
NLP(三):Attention
http://hemingwang.blogspot.com/2019/01/attention.html
NLP(四):ConvS2S
https://hemingwang.blogspot.com/2019/04/convs2s.html
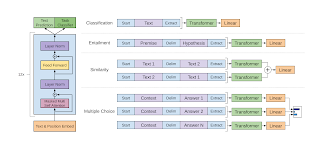
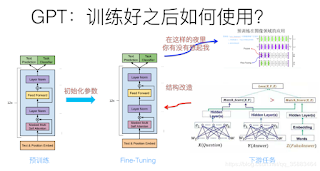
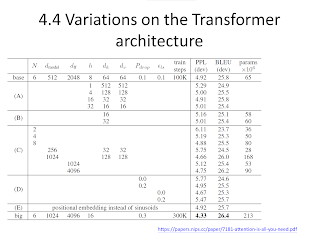
NLP(五):Transformer
http://hemingwang.blogspot.com/2019/01/transformer.html
-----
四、附錄
(一):Space
https://hemingwang.blogspot.com/2019/04/mathspace.html
(二):如何學好英文
https://hemingwang.blogspot.com/2020/07/learning-english.html
(三):如何撰寫論文
https://sanmin.com.tw/Product/index/000758374